Geometrie pentru școala elementară/Unghiuri
În această secțiune, vom vorbi despre unghiuri.
Unghiuri
[modificare]
Un unghi (∠) este alcătuit dintr-un vârf (punct), două brațe (raze) și un arc. Acestea sunt aranjate astfel încât extremitatea comună a brațelor coincide cu vârful, iar arcul se construiește de la un braț la altul. Dimensiunea unui unghi depinde de cât de mult sunt deschise brațele, iar unghiurile sunt măsurate în grade. Aveți posibilitatea să le măsoare prin punerea pe protractor vârful și se uită la grade a doua braț a ajuns.
Un unghi care este mai mic de 90 ° este cunoscut sub numele de unghi ascuțit. Un unghi de 90° este cunoscut sub numele de unghi drept. Acelea între 90° și 180° sunt unghiuri obtuze. La exact 180° unghiurile se numesc unghiuri cu laturi în prelungire. Acelea între 180° și 360° sunt unghiuri reflexe, în timp ce unghiuri la 360 ° sunt unghiuri rotunde
Un unghi este de obicei numit de puncte pe care el însuși le conține. Formatul este după cum urmează:
- "∠" + un punct de pe un braț + vârf (punct) + un punct de pe celălalt braț
Cu toate acestea, uneori, nu există unghiuri pe acel vârf, și putem omite punctele de pe brațe. De fapt, atunci când suntem leneși, putem folosi chiar și o literă mică pentru a reprezenta un anumit unghi. Rețineți că, în acest caz, trebuie să fie omis semnul ∠. Deși o literă minusculă reprezintă valoarea unghiului, toate aceste denumiri pot fi folosite ca necunoscute în ecuații.
'Unghiuri adiacente' (adj ∠s.) Sunt unghiuri în cazul în care: brațele opuse coincid #Their (suprapunere); arce #Their nu coincid (suprapunere); nodurile #Their coincid (suprapunere).
Uneori, două unghiuri pot adăuga până la 90 ° sau 180 °. Ele se numesc unghiuri complementare și unghiuri complementare, respectiv. Cât mai multe unghiuri au astfel de proprietăți, acestea vor fi destul de la îndemână în viitor.
Unghiuri la un punct
[modificare]
Uneori, două sau mai multe unghiuri au un vârf comun, iar dimensiunile lor se însumează până la 360 o. Ele se numesc unghiuri la un punct. Acest lucru poate fi foarte util atunci când vom scrie dovezi sau afla unghiuri.
De exemplu, imaginați-vă că O este un punct într-o figură dată. Cele trei puncte, A, B și respectiv C sunt in jurul punctului O, și câte o rază/linie duce de la O la A, B și C. Având în vedere faptul că ∠AOB=120° și ∠BOC=150°,
Unghiuri adiacente pe o linie dreaptă
[modificare]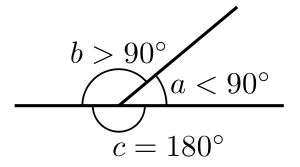
Când dimensiunile unghiuri adiacente au suma egală cu 180 °, acestea sunt unghiuri adiacente de pe o linie dreaptă. Ele sunt folosite la aflarea valorii unuia dintre unghiurile. (Sau mai mult, pentru care contează, atunci când au unghiuri care sunt egale sau conexe.) Abrevierea, adj. ∠s pe st. line, poate fi folosit ca referință care unghiurile adăuga până la 180 °.
Uită-te la imaginea de pe dreapta ca un exemplu. Aici, b și o sunt suplimentare. Suma b și o este egal cu c . B și o sunt unghiuri adiacente de pe o linie dreaptă. Dacă știm valoarea b , putem afla valoarea o cu ușurință. Rețineți că o , b și c sunt unghiuri într-un punct.
Unghiuri opuse vertical
[modificare]
Unghiurile opuse vertical sunt foarte simple. În cazul în care două linii drepte rulează una peste alta, unghiurile opuse produse pot să fie numite unghiuri opuse vertical. Ele trebuie să fie egale între ele. Rețineți că nu puteți presupune că ceva este o linie dreaptă doar prin observație, astfel încât să fie sigur că este menționat în întrebare, înainte de a face ceva. Unghiuri opuse este Vertically o referință foarte comună și va veni la îndemână în multe situații, așa că înainte de a se blocat pe o problemă, a se vedea dacă puteți găsi unele unghiuri pe verticală opuse mai întâi.
Uită-te la figura din partea dreaptă. După cum se indică în această figură, D este egal cu C și A este egal cu B . Acest lucru se datorează faptului că acestea sunt unghiuri opuse vertical. Rețineți că aici, D și A , A și C , C și B și D și B sunt toate perechi de unghiuri adiacente de pe o linie dreaptă. De asemenea, cele patru unghiuri sunt unghiuri la un punct.

