Studiul anumitor procese, fenomene impune considerarea variației unei mărimi fizice în raport cu alta.
De exemplu, în studiul mișcării se poate considera variația unei coordonate de pe traiectorie în raport de timpul și se spune că acea coordonată este o funcție de timp.
Definiție .
Dacă printr-un procedeu se poate face ca unei variabile
x
∈
D
{\displaystyle x\in D}
y
∈
E
,
{\displaystyle y\in E,}
funcție de pe mulțimea
D
{\displaystyle D}
domeniu ) pe mulțimea
E
{\displaystyle E}
codomeniu ) și se notează
f
:
D
→
E
,
{\displaystyle f:D\to E,}
y
=
f
(
x
)
.
{\displaystyle y=f(x).}
Exemplu .
Funcția care stabilește valoarea
A
{\displaystyle A}
cerc de rază
r
{\displaystyle r}
A
:
R
→
R
,
A
(
r
)
=
π
r
2
.
{\displaystyle A:\mathbb {R} \to \mathbb {R} ,\;A(r)=\pi r^{2}.}
O funcție poate fi reprezentată prin diagrame, prin tabel, printr-un grafic sau analitic.
Diagramă reprezentând o funcție cu domeniul
{
1
,
2
,
3
,
4
}
{\displaystyle \{1,2,3,4\}}
{
a
,
b
,
c
,
d
}
{\displaystyle \{a,b,c,d\}}
Prin acest mod de reprezentare se indică faptul că valorilor
x
1
,
x
2
,
⋯
,
x
n
{\displaystyle x_{1},x_{2},\cdots ,x_{n}}
x
{\displaystyle x}
y
1
,
y
2
,
⋯
,
y
n
{\displaystyle y_{1},y_{2},\cdots ,y_{n}}
y
:
{\displaystyle y:}
x
{\displaystyle \mathbf {x} }
x
1
{\displaystyle x_{1}}
x
2
{\displaystyle x_{2}}
⋯
{\displaystyle \cdots }
x
n
{\displaystyle x_{n}}
y
{\displaystyle \mathbf {y} }
y
1
{\displaystyle y_{1}}
y
2
{\displaystyle y_{2}}
⋯
{\displaystyle \cdots }
y
n
{\displaystyle y_{n}}
Graficul unei funcţii
f
:
R
→
R
.
{\displaystyle f:\mathbb {R} \to \mathbb {R} .}
În cazul funcțiilor
f
:
A
⊆
R
→
R
,
f
(
x
)
=
y
,
{\displaystyle f:A\subseteq \mathbb {R} \to \mathbb {R} ,\;f(x)=y,}
reprezentarea grafică se realizează cu ajutorul unui sistem de coordonate rectangulare
x
O
y
,
{\displaystyle xOy,}
O
x
{\displaystyle Ox}
x
,
{\displaystyle x,}
O
y
{\displaystyle Oy}
y
.
{\displaystyle y.}
În cazul funcțiilor de două variabile, de forma
z
=
f
(
x
,
y
)
,
{\displaystyle z=f(x,y),}
O
x
y
z
.
{\displaystyle Oxyz.}
[ modificare ] Acest tip de scriere a unei funcții face apel la expresia matematică ce definește corespondența dintre argument și valoarea funcției în acel punct.
Exemple:
f
(
x
)
=
sin
x
,
g
(
x
)
=
x
−
1
x
2
+
1
,
φ
(
x
)
=
2
x
−
5
+
3
x
.
{\displaystyle f(x)=\sin x,\;g(x)={\frac {x-1}{x^{2}+1}},\;\varphi (x)=2^{x}-{\sqrt {5+3x}}.}
Se consideră funcțiile
f
:
D
→
E
{\displaystyle f:D\to E}
g
:
E
→
F
.
{\displaystyle g:E\to F.}
g
∘
f
:
D
→
F
{\displaystyle g\circ f:D\to F}
g
∘
f
(
x
)
=
d
e
f
g
(
f
(
x
)
)
,
∀
x
∈
D
,
{\displaystyle g\circ f(x){\overset {\underset {\mathrm {def} }{}}{=}}g(f(x)),\;\forall x\in D,}
se numește compunerea funcțiilor
f
,
g
.
{\displaystyle f,g.}
Observații.
(i) În general, compunerea a două funcții nu este comutativă (dacă este posibilă în ambele sensuri).(ii) Pentru a putea compune funcțiile
f
,
g
{\displaystyle f,g}
f
{\displaystyle f}
g
.
{\displaystyle g.}
O funcție
f
:
D
→
E
{\displaystyle f:D\to E}
injectivă dacă
∀
x
,
y
∈
D
,
x
≠
y
⇒
f
(
x
)
≠
f
(
y
)
.
{\displaystyle \forall x,y\in D,\;x\neq y\;\Rightarrow \;f(x)\neq f(y).}
O funcție
f
:
D
→
E
{\displaystyle f:D\to E}
surjectivă dacă
∀
y
∈
E
,
∃
x
∈
D
astfel încât
y
=
f
(
x
)
.
{\displaystyle \forall y\in E,\;\exists x\in D\;{\text{ astfel încât }}y=f(x).}
O funcție
f
:
D
→
E
{\displaystyle f:D\to E}
bijectivă dacă este injectivă și surjectivă.
În acest caz, se spune că mulțimile
D
,
E
{\displaystyle D,E}
O funcție
f
:
D
→
E
{\displaystyle f:D\to E}
inversabilă dacă există o funcție
f
−
1
:
E
→
D
{\displaystyle f^{-1}:E\to D}
(i)
f
−
1
∘
f
(
x
)
=
x
,
∀
x
∈
D
;
{\displaystyle f^{-1}\circ f(x)=x,\;\forall x\in D;}
(ii)
f
∘
f
−
1
(
y
)
=
y
,
∀
y
∈
E
.
{\displaystyle f\circ f^{-1}(y)=y,\;\forall y\in E.}
Câteva funcții elementare (care vor fi studiate ulterior detaliat) sunt:
funcția putere :
f
:
R
→
R
,
f
(
x
)
=
x
α
,
{\displaystyle f:\mathbb {R} \to \mathbb {R} ,\;f(x)=x^{\alpha },}
α
>
0
;
{\displaystyle \alpha >0;}
funcția exponențială :
f
:
R
→
R
+
,
f
(
x
)
=
a
x
,
{\displaystyle f:\mathbb {R} \to \mathbb {R} _{+},\;f(x)=a^{x},}
a
>
0.
{\displaystyle a>0.}
funcția logaritmică :
f
:
(
0
,
∞
)
→
R
,
f
(
x
)
=
log
a
x
,
{\displaystyle f:(0,\infty )\to \mathbb {R} ,\;f(x)=\log _{a}x,\;}
a
>
0
;
{\displaystyle a>0;}
funcțiile trigonometrice :
sinus :
y
=
sin
x
,
{\displaystyle y=\sin x,}
cosinus :
y
=
cos
x
,
{\displaystyle y=\cos x,}
tangentă :
y
=
tan
x
,
{\displaystyle y=\tan x,}
cotangentă :
y
=
cot
x
;
{\displaystyle y=\cot x;}
funcțiile trigonometrice inverse:
y
=
arcsin
x
,
y
=
arccos
x
,
y
=
arctan
x
.
{\displaystyle y=\arcsin x,\;y=\arccos x,\;y=\arctan x.}
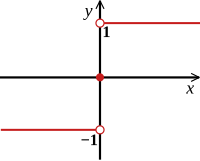
Graficul funcţiei signum funcția signum (funcția semn ):
sgn
:
R
→
{
−
1
,
0
,
1
}
{\displaystyle \operatorname {sgn} :\mathbb {R} \to \{-1,0,1\}}
sgn
(
x
)
=
{
−
1
dacă
x
<
0
,
0
dacă
x
=
0
,
1
dacă
x
>
0.
{\displaystyle \operatorname {sgn}(x)={\begin{cases}-1&{\text{dacă }}x<0,\\0&{\text{dacă }}x=0,\\1&{\text{dacă }}x>0.\end{cases}}}
I. Noţiuni introductive
1. Mulțimi, numere, structuri
2. Sisteme de ecuații liniare
3. Funcții elementare
II. Calculul
1. Șiruri și serii
2. Funcții: limite și continuitate
3. Derivate și diferențiale
4. Șiruri și serii de funcții
5. Funcții de mai multe variabile
6. Funcții implicite
7. Schimbări de variabile
III. Calculul
1. Integrale definite și nedefinite
2. Extinderea noțiunii de integrală definită
3. Integrale curbilinii
4. Integrale duble și de suprafață
5. Integrale triple
IV. Ecuații
diferențiale
1. Ecuații diferențiale de ordinul întâi
2. Ecuații diferențiale de ordin superior
3. Sisteme de ecuații diferențiale
4. Ecuații cu derivate parțiale de ordinul întâi
Cu "ex" sunt notate paginile cu exerciţii referitoare la paragraful respectiv.