Analiză matematică/Numere reale

Conceptul de număr reprezintă o noțiune de bază a matematicii. Un număr rațional poate fi exprimat atât sub formă de fracție, cât și sub formă zecimală, fie cu un număr finit de zecimale, fie cu zecimale care se repetă periodic. Exemple:

$0={\frac {0}{1}},\quad 1={\frac {1}{1}},\quad 1,25={\frac {5}{4}},\quad 0,(1)={\frac {1}{9}}.$

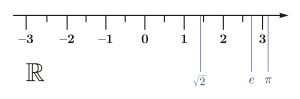
Reprezentarea pe dreaptă a numerelor reale

Un mod de exprimare a numerelor reale îl constituie scrierea zecimală. De exemplu:

$5=5,000\cdots$

$-{\frac {3}{4}}=-0,75000\cdots$

${\sqrt {2}}=1,4142\cdots$

$\pi =3,14159\cdots$

Punctele de suspensie indică faptul că zecimalele se continuă în mod indefinit, lucru care are loc în cazul numerelor iraționale.

Numerele reale se pot reprezenta geometric ca puncte ale unei drepte.

Număr natural

Conceptul de număr natural stă la baza întregii matematici şi cu ajutorul acestuia se va defini ulterior mulţimea numerelor reale. Mulţimea numerelor naturale poate fi definită axiomatic cu ajutorul axiomelor lui Peano.

Axiomele lui Peano Se numeşte mulţime a numerelor naturale o mulţime A pe care s-a definit o aplicaţie $A\ni x\mapsto x^{*}\in A,$ numită lege de succesiune pe A şi care satisface proprietăţile: Axioma I. În A s-a distins un element numit prim element al lui A, notat cu 1 (sau 0). Axioma II. Legea de succesiune pe A este o injecţie a mulţimii A în mulţimea $A\setminus \{1\}.$ Axioma III. Fie B o mulţime cu proprietăţile: $(i)\;1\in B;\;(ii)\;x\in b\Rightarrow \;x^{*}\in B.$ Atunci $B=A.$

Proprietăți ale numerelor reale

Proprietățile numerelor reale sunt de trei tipuri

• algebrice: numerele reale se pot aduna, scădea, înmulți, împărți (în acest ultim caz trebuie că împărțitorul să fie nenul), rezultatul fiind tot un număr real.
• de ordine: dându-se două numere reale $x,y,$ este valabilă una din inegalitățile: $x\leq y$ sau $y\leq x.$
• de completitudine.

Proprietăți algebrice

Pe mulțimea numerelor reale se definesc două operații de bază: adunarea și înmulțirea.

Proprietățile adunării numerelor reale 1) $a+b=b+a,\;\forall a,b\in \mathbb {R}$ (comutativitate) 2) $(a+b)+c=a+(b+c),\;\forall a,b,c\in \mathbb {R}$ (asociativitate) 3) $\exists 0\in \mathbb {R}$ a.î. $\;a+0=0+a=a,\;\forall a\in \mathbb {R}$ (existență element neutru) 4) $\forall a\in \mathbb {R} \;\exists (-a)\in \mathbb {R} \;$ a.î. $a+(-a)=0$ (existență element opus).

Proprietățile înmulțirii numerelor reale 1) $a\cdot b=b\cdot a,\;\forall a,b\in \mathbb {R}$ (comutativitate) 2) $(a\cdot b)\cdot c=a\cdot (b\cdot c),\;\forall a,b,c\in \mathbb {R}$ (asociativitate) 3) $\exists 1\in \mathbb {R}$ a.î. $\;a\cdot 1=1\cdot a=a,\;\forall a\in \mathbb {R}$ (existență element neutru) 4) $\forall a\in \mathbb {R} \setminus \{0\}\;\exists a^{-1}={\frac {1}{a}}\in \mathbb {R} \;$ a.î. $a\cdot {\frac {1}{a}}=1$ (existență element opus). 5) $(a+b)\cdot c=a\cdot c+b\cdot c$ (distributivitate față de adunare).

Structura de ordine

Proprietățile inegalității. Dacă $a,b,c\in \mathbb {R} ,$ atunci: 1. $a<b\;\Rightarrow \;a+c<b+c;$ 2. $a<b\;\Rightarrow \;a-c<b-c;$ 3. $a<b$ și $c>0\;\Rightarrow \;ac<bc;$ 4. $a<b$ și $c<0\;\Rightarrow \;ac>bc;$  în particular, $-a>-b;$

Teoremă. Orice număr real $\alpha$ poate fi exprimat, la un anumit grad de precizie, cu ajutorul numerelor raționale.

Într-adevăr, fie $\alpha >0$ un număr irațional și se pune problema aproximării acestuia cu o precizie de ${\frac {1}{n}}$ (cum ar fi ${\frac {1}{10^{n}}},\;{\frac {1}{100}},\cdots$). Există un $N\in \mathbb {Q}$ astfel încât $N\leq \alpha \leq N+1.$ Se divide intervalul $[N,N+1]$ în $n$ părți. Atunci $\alpha$ se situează într-un interval de tip $\left[N+{\frac {m}{n}},N+{\frac {m+1}{n}}\right].$

Exemplu. Numărul irațional ${\sqrt {2}}$ poate fi aproximat prin numere raționale astfel:

$1,4<{\sqrt {2}}<1,5$ cu precizie de o zecimală;

$1,41<{\sqrt {2}}<1,42$ cu precizie de două zecimale;

$1,414<{\sqrt {2}}<1,415$ cu o precizie de trei zecimale etc.

Valoare absolută

Definiție. Valoarea absolută (sau modulul) unui număr $a\in \mathbb {R}$ este:

$|a|={\begin{cases}\;a,&dac{\breve {a}}\;a\geq 0\\-a,&dac{\breve {a}}\;a<0\end{cases}}$

Proprietăți. Dacă $x,y\in \mathbb {R} ,$ atunci:

1) $|x+y|\leq |x|+|y|;$

2) $|x-y|\leq |x|-|y|;$

3) $|xy|=|x|\cdot |y|;$

4) $\left|{\frac {x}{y}}\right|={\frac {|x|}{|y|}},\quad (y\neq 0).$

Demonstrație.

1) Avem cazurile:

a) $x+y\geq 0.$   Atunci $|x+y|=x+y\leq |x|+|y|$  (deoarece $x\leq |x|$ și $y\leq |y|.$)

b) $x+y<0.$   Atunci $|x+y|=-(x+y)=(-x)+(-y)\leq |x|+|y|.$

2) Fie $x-y=z,$ atunci $x=y+z$ și se folosește punctul anterior:

$|x|=|y+z|\leq |y|+|z|=|y|+|x-y|,$ deoarece $|x|-|y|\leq |x-y|.$

Binomul lui Newton

Dacă $a,b\in \mathbb {R}$ și $n\in \mathbb {N} ^{*},$ atunci:

$(a+b)^{n}=a^{n}+na^{n-1}b+{\frac {n(n-1)}{2!}}a^{n-2}b^{2}+{\frac {n(n-1)(n-2)}{3!}}a^{n-3}b^{3}+\cdots b^{n},$

sau, dacă definim coeficienții binomiali: $C_{n}^{k}={\frac {n!}{k!(n-k)!}},$

atunci se mai poate scrie:

$(a+b)^{n}=\sum _{k=0}^{n}a^{n-k}b^{k}.$

Forma generalizată a binomului lui Newton:

Dacă $a,b\in \mathbb {R}$ astfel încât $|b/a|<1,$ iar $\alpha \in \mathbb {R} ,$ atunci:

$(a+b)^{\alpha }=a^{\alpha }\left(1+{\frac {b}{a}}\right)^{\alpha }=$

$=a^{\alpha }\left(1+{\frac {\alpha }{1!}}\left({\frac {b}{a}}\right)+{\frac {\alpha (\alpha -1)}{2!}}\left({\frac {b}{a}}\right)^{2}+{\frac {\alpha (\alpha -1)(\alpha -2)}{3!}}\left({\frac {b}{a}}\right)^{3}+\cdots \right)$

Exemplu. Să se dezvolte $(3+x)^{-1/2},$ stabilind acele valori ale lui $x$ pentru care seria obținută este convergentă.

Soluție. Punând ${\frac {b}{a}}={\frac {1}{3}}x,$ se obține:

$(3+x)^{-1/2}=3^{-1/2}\left(1+{\frac {1}{3}}x\right)^{-1/2}={\frac {1}{\sqrt {3}}}\left(1-{\frac {1}{6}}x+{\frac {1}{24}}x^{2}-{\frac {5}{432}}x^{3}+\cdots \right)$

Seria converge dacă $|{\frac {1}{3}}x|<1,$ echivalent cu $|x|<3.$

Inegalități remarcabile

Inegalitatea mediilor

Fie $a_{1},a_{2},\cdots ,a_{n}\in \mathbb {R} _{+}^{*},\;i={\overline {1,n}},\;n\in \mathbb {N} ^{*}.$ Atunci:

${\frac {a_{1}+a_{2}+\cdots +a_{n}}{n}}\geq {\sqrt[{n}]{a_{1}a_{2}\cdots a_{n}}}\geq {\frac {n}{{\frac {1}{a_{1}}}+{\frac {1}{a_{2}}}+\cdots +{\frac {1}{a_{n}}}}}$   (Inegalitatea mediilor).

Pentru demonstrația acesteia se va utiliza următoarea lemă:

Lemă. Fie $a_{i}\in \mathbb {R} _{+},\;i={\overline {1,n}}\;(n\in \mathbb {N} ^{*})$ cu proprietatea $\prod _{i=1}^{n}a_{1}=1.$ Atunci $\sum _{i=1}^{n}a_{i}\geq n,$ egalitatea având loc dacă și numai dacă $a_{1}=a_{2}=\cdots =a_{n}=1.$

Demonstrația lemei. Se utilizează inducția matematică. Pentru $n=1$ lema este evidentă. Se presupune că afirmația din lemă este adevărată pentru $n\in \mathbb {N} ^{*}$ și se demonstrează pentru $n+1.$ Fie deci $a_{i}\in \mathbb {R} _{+},\;i={\overline {1,n+1}}$ cu $\prod _{i=1}^{n}a_{i}=1.$ Printre aceste numere există unele mai mici sau egale cu 1 și altele mai mari sau egale cu 1. Renumerotându-le, se poate presupune că $a-1\leq 1,\;a_{2}\geq 1.$ Atunci:

$(a_{1}-1)(a_{2}-1)\leq 0,$ ceea ce este echivalent cu:

$a_{1}a_{2}+\leq a_{1}+a_{2}.$

Deoarece $(a_{1}a_{2})a_{3}\cdots a_{n}=1,$ aplicând lema pentru $n$ numere, se deduce că:

$a_{1}a_{2}+a_{3}+\cdots +a_{n+1}\geq n,$

cu egalitate pentru $a_{1}a_{2}=a_{3}=\cdots =a_{n+1}=1.$

Rezultă că:

$(a_{1}+a_{2})+a_{3}+\cdots +a_{n+1}\geq a_{1}a_{2}+1+a_{3}+\cdots +a_{n+1}\geq n+1,$ adică $\sum _{i=1}^{n+1}\geq n+1,$

cu egalitate pentru $a_{1}=a_{2}=\cdots =a_{n+1}=1.$

Conform metodei inducției matematice, lema este demonstrată.

Pentru demonstrarea inegalității mediilor, se aplică lema pentru numerele:

$x_{i}={\frac {a_{i}}{\sqrt[{n}]{{\underset {i=1}{\overset {n}{\prod }}}a_{i}}}},\qquad i={\overline {1,n}}.$

Caz particular.

Dacă $a,b\in (0,+\infty ),$ atunci: ${\frac {a+b}{2}}\geq {\sqrt {ab}}\geq {\frac {2ab}{a+b}}.$

Inegalitatea lui Bernoulli

Fie $a_{1},a_{2},\cdots ,a_{n}\in (-1,\infty ),\;i\in {\overline {1,n}},\;n\in \mathbb {N} ^{*}.$ Atunci:

$(1+a_{1})(1+a_{2})\cdots (1+a_{n})\geq 1+a_{1}+a_{2}+\cdots +a_{n}.$

Inegalitatea Cauchy-Buniakowski-Schwarz

Fie $a_{i},b_{i}\in \mathbb {R} ,\;i={\overline {1,n}},\;n\in \mathbb {N} ^{*}.$ Atunci:

$\sum _{i=1}^{n}|a_{i}b_{i}|\leq \left(\sum _{i=1}^{n}a_{i}^{2}\right)^{\frac {1}{2}}\cdot \left(\sum _{i=1}^{n}b_{i}^{2}\right)^{\frac {1}{2}}.$

Inegalitatea lui Cebîșev

Fie $a_{1},a_{2},\cdots ,a_{n}$ și $b_{1},b_{2},\cdots ,b_{n}$ numere reale cu:

$a_{1}\geq a_{2}\geq \cdots \geq a_{n},\quad b_{1}\geq b_{2}\geq \cdots b_{n}.$

Atunci:

$a_{1}b_{n}+a_{2}b_{n-1}+\cdots +a_{n}b_{1}\leq a_{1}b_{i_{1}}+a_{2}b_{i_{2}}+\cdots +a_{n}b_{in}\leq a_{1}b_{1}+a_{2}b_{2}+\cdots a_{n}b_{n}.$

Demonstrație. Fie $j<k,\;i_{j}<i_{k}.$ Atunci $(a_{j}-a_{k})(b_{i_{j}}-b_{ik})\geq 0$ implică: $a_{j}b_{i_{j}}+a_{k}b_{i_{k}}\geq a_{j}b_{i_{k}}+a_{k}b_{i_{j}}.$

Rezumat

mulţimea numerelor naturale: $\mathbb {N} =\{1,2,3,\cdots \}.$ mulţimea numerelor întregi: $\mathbb {Z} =\{\cdots ,-3,-2,-1,0,1,2,3,\cdots \}.$ mulţimea numerelor întregi negative: $\mathbb {Z} ^{-}=\{\cdots ,-3,-2,-1\}.$ mulţimea numerelor raţionale: $\mathbb {Q} =\{x\;|\;x{\frac {a}{b}}\land a\in \mathbb {Z} \land b\in \mathbb {Z} \land b\neq 0\}.$ numerele iraţionale: conţin zecimale care nu se repetă şi care nu sunt în număr finit. mulţimea numerelor reale: $\mathbb {R}$ mulţimea numerelor complexe: $\mathbb {C} =\{x+\mathbf {i} y\;|\;x\in \mathbb {R} \land y\in \mathbb {R} \}.$ $\mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset C.$